克里金法

n克里金法是一种用于空间插值的地统计学方法。与前面介绍的其它插值法相比，克里金法可用估计的预测误差来评估预测的质量。

n克里金法假设某种属性的空间变异既不是完全随机性的也不是完全确定性的。相反，空间变异可能包括三种影响因素：表征区域变量变异的空间相关因素；表征趋势的“漂移”或结构；还有随机误差。

n对几种影响的不同解释，形成用于空间插值的不同克里金法。

半变异图

n克里金法用半变异测定空间相关要素，这里的要素是指对空间依赖的要素或称之空间自相关要素。

n相对于数据集中各对已知点的距离点绘半变异云图。如果数据集不存在空间相关，那么近距离已知点之间的半变异很小，相反，较远距离的已知点之间的半变异较大。

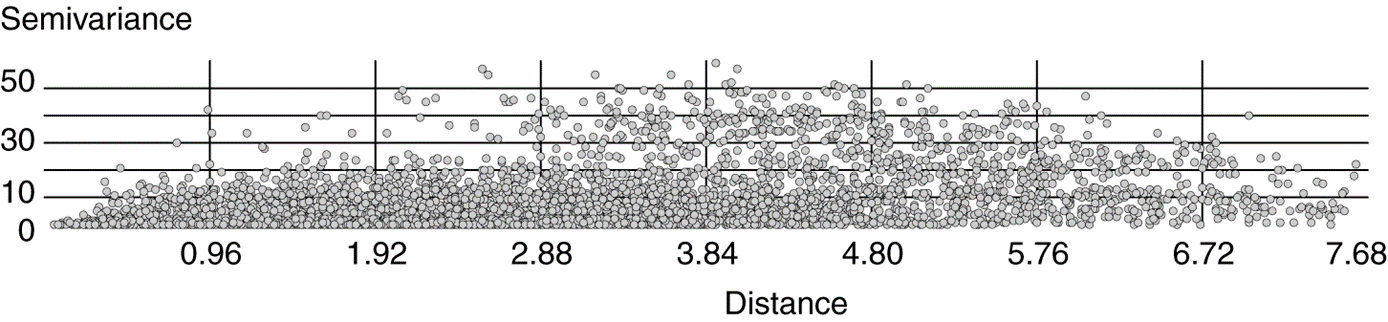
                      图15.14  

                       半变异云图。

区间分组（binning）

半变异云图包含所有的控制点对，使之操作和使用不方便。区间分组（binning）的过程，是以距离和方向来平均半变异数据。

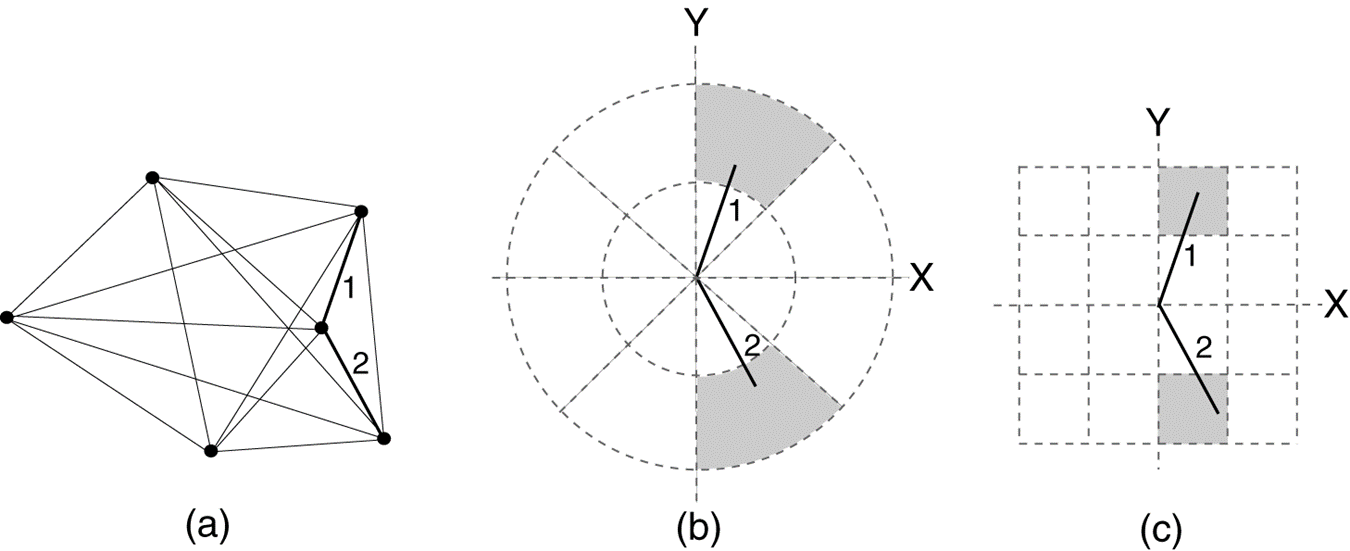
                       图15.15  

对图（a）中的1和2样本按方向进行区间归类的常用方法是径向扇区（b）。ArcGIS中的Geostatistical Analyst 则使用如图（c）的格网像元。

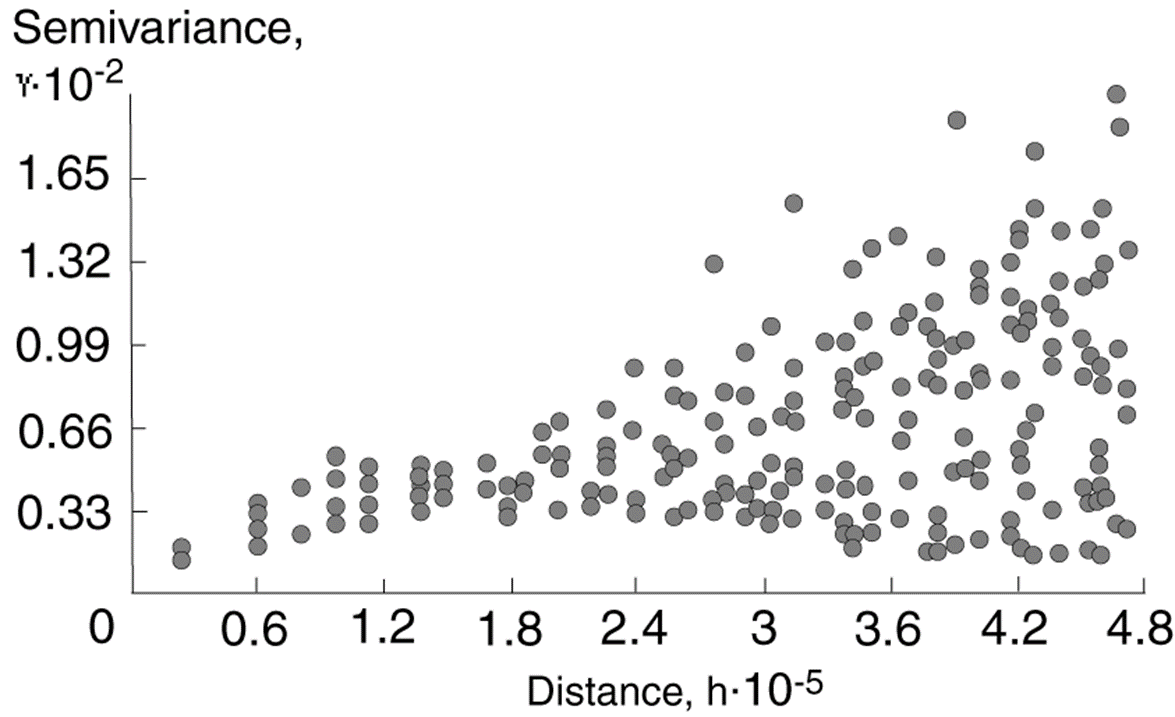
                       图15.16 

通过距离区间分组后的半变异图。

模型拟合

半变异图通常须用某一数学函数或模型来拟合。拟合的半变异图可用于估算任意给定距离的半变异。

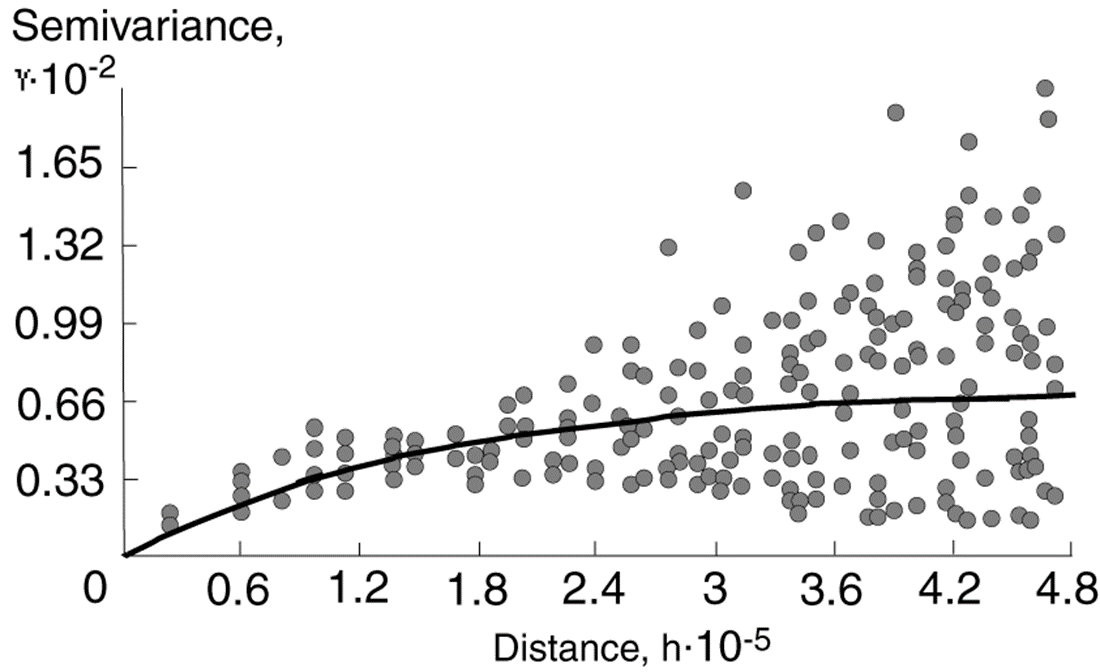
                      图15.17  

用数学函数或模型拟合半变异。

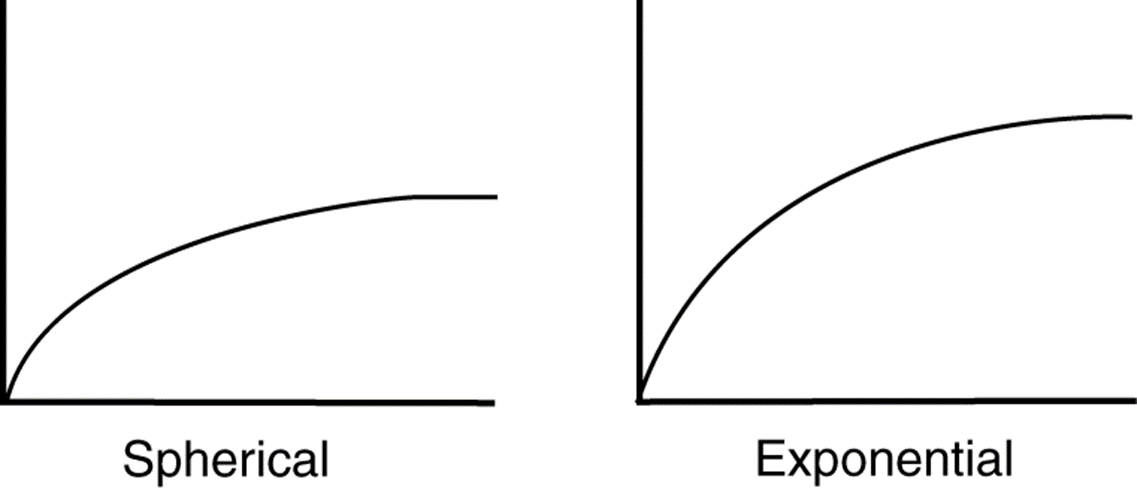
                      图15.18 

拟合半变异图的两种常见模型：球体模型和指数模型。

块金(nugget)、变程(range)和总基台值（sill）

n块金(nugget)是样对距离为0时的半变异，表示测量及分析误差或微小变异，或两者。

n变程(range)是半变异开始稳定时的样对距离。

n超过该变程，半变异趋平于相对恒定值。此时的半变异称为总基台值（sill）

                        图15.19 

块金、变程、总基台值和基台值。

普通克里金法（Ordinary Kriging）

假设不存在漂移，普通克里金法重点考虑空间相关的因素，并用拟合的半变异直接进行插值。

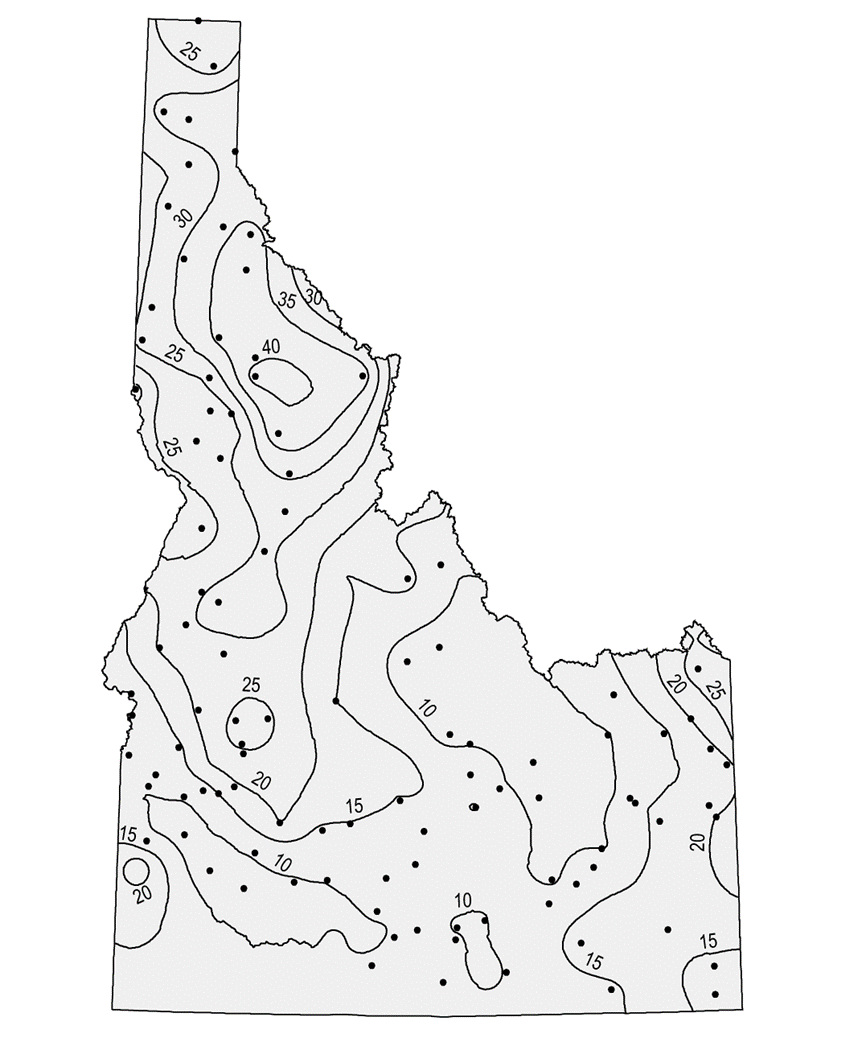
                       图15.20 

基于指数模型的普通克里金插值法生成的等雨量线图。

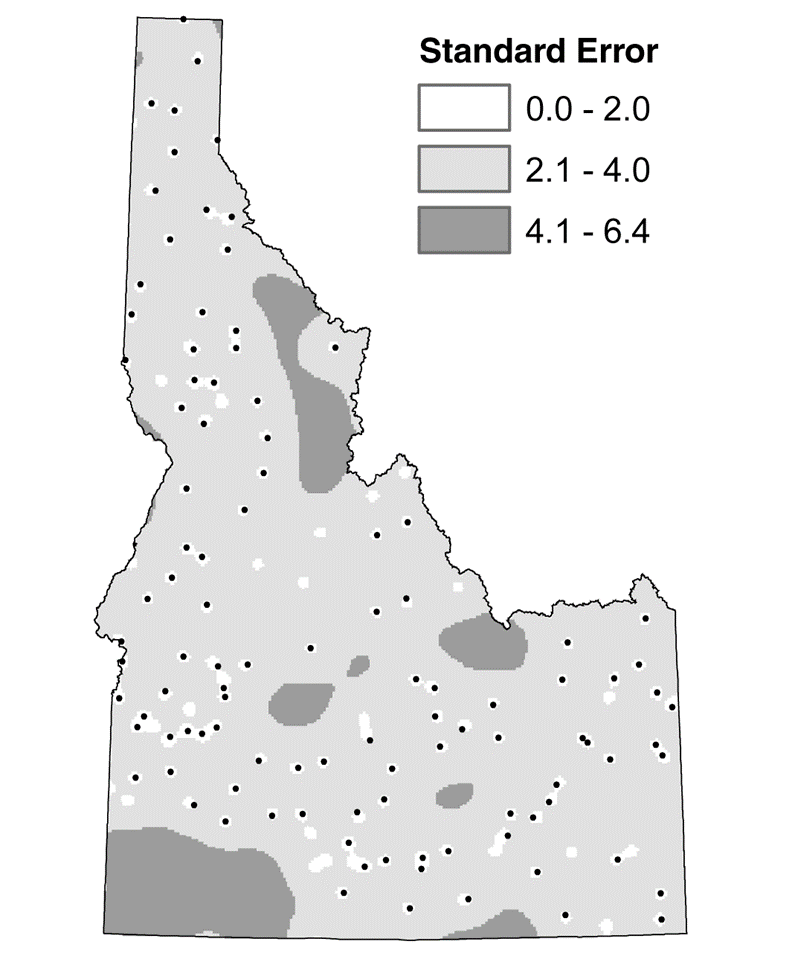
                       图15.21   

图15.20中的年降水量曲面的标准误差。

泛克里金法（Universal Kriging）

泛克里金法假设除了样本点之间的空间相关性外，空间变量的z值还受到漂移或倾向等影响。

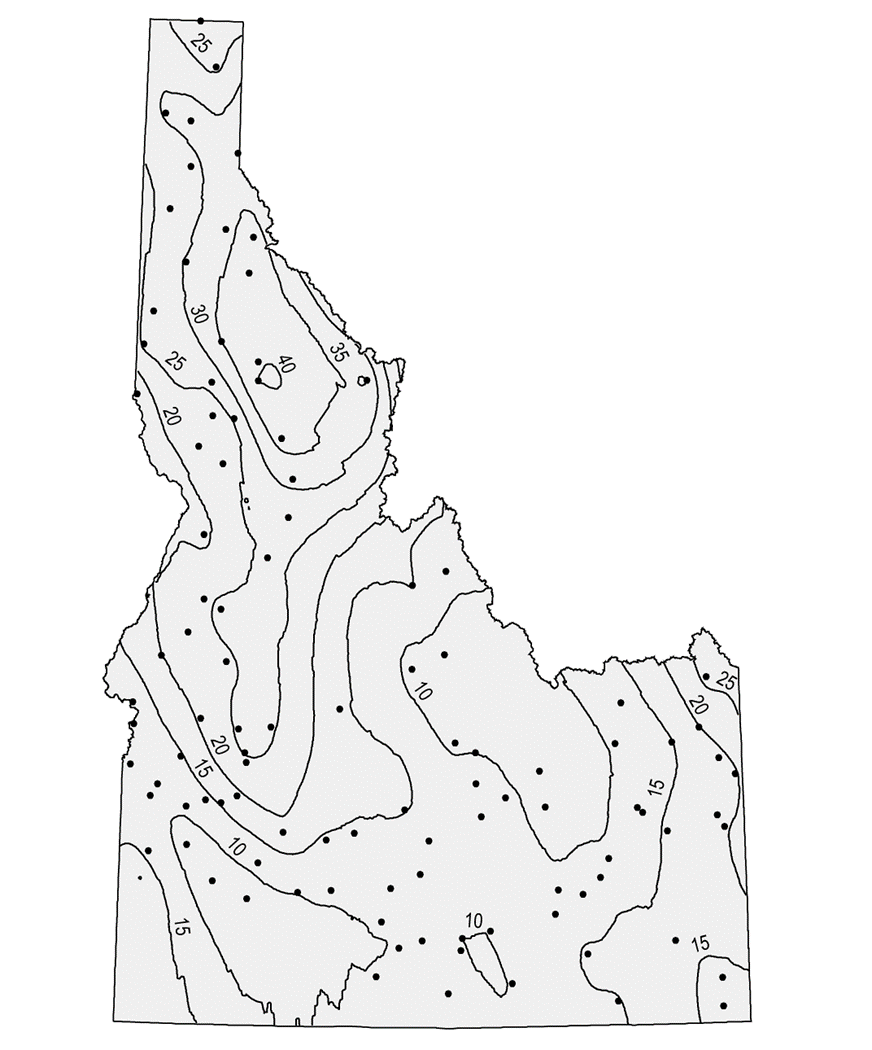
                       图15.22

基于线性漂移和球体模型的泛克里金插值法的等雨量线图。

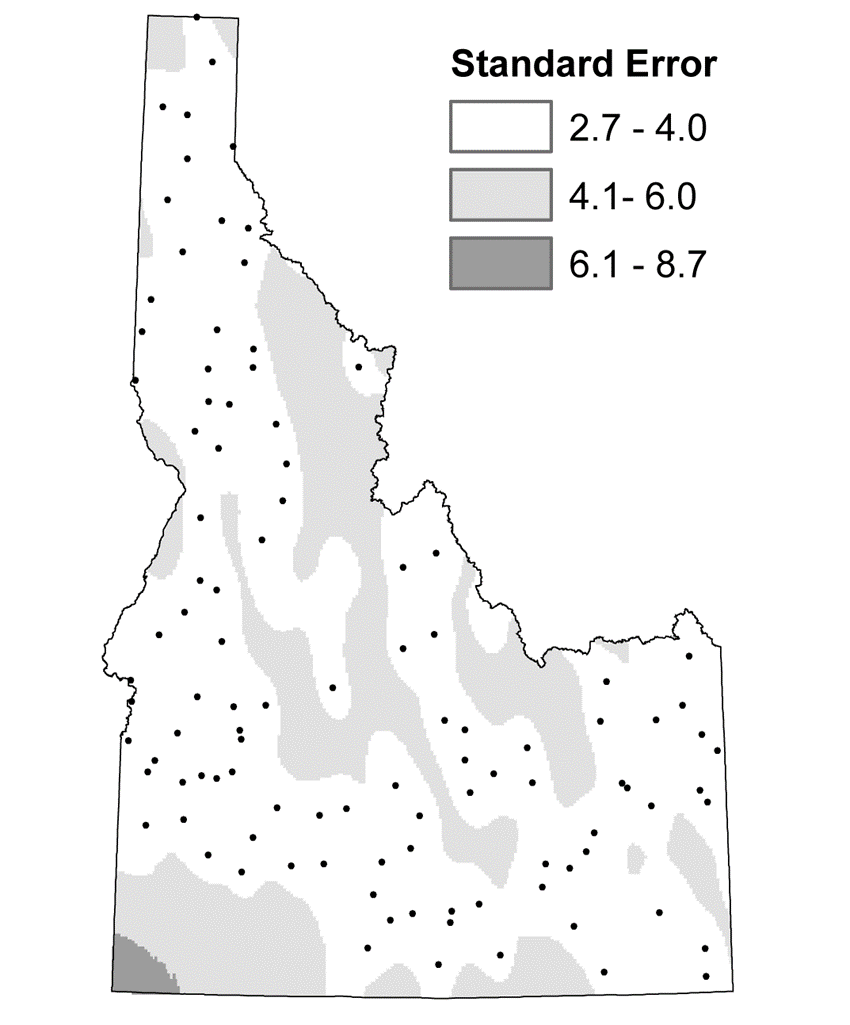
                       图15.23 

图15.22中年降水量曲面的标准差分布图。

其它克里金法

除了普通克里金和泛克里金外，其它克里金法包括指示性克里金法、离析克里金法和块克里金法