一、B样条曲线的历史
1946年,schoenbeg( 舍恩伯格 )提出样条的概念
1972年, de Boor和Cox分别提出了B样条的计算方法
1974年,Gordon和Riesenfeld将B样条理论用于形状描述,提出了B样条曲线和曲面
二、B样条曲线的定义
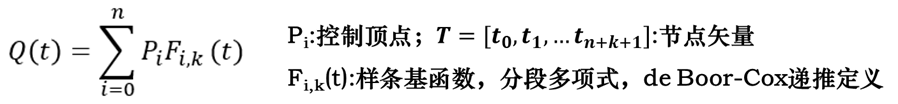
B样条曲线分类(依据节点矢量中节点分布情况):
均匀B样条曲线(Uniform B-Spline Curve)- 节点均与分布
准均匀B样条曲线(Quasi-uniform B-Spline Curve)- 两端节点重复度k+1
分段Bezier曲线(Piecewise Bezier Curve)- 两端节点重复度k+1,内节点重复度k
非均匀B样条曲线(Non-uniform B-Spline Curve)- 节点非递减,两端节点重复度≤k+1,内节点重复度≤k
均匀B样条定义:
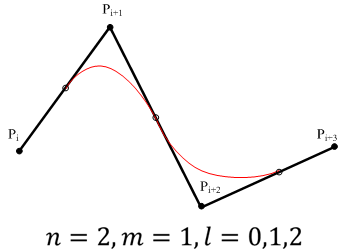
若给定m+n+1个控制顶点Ph(h=0,1,2,…,m+n) ,则第i段(i=0,1, …,m,共m+1段)、n次等距分割的B样条曲线函数为
![]()
Fl,n(t)为第i段,n次B样条基函数(B样条分段混合函数)
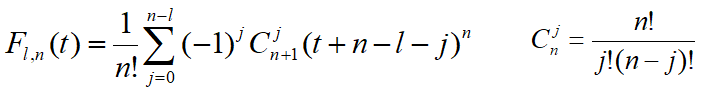
Pi+l为定义第i段曲线的特征多边形的n+1个顶点(l=0,1,2,…n)。
说明:
B样条曲线是分段定义的。如果给定 m+n+1 个顶点 Ph ,则可定义 m+1 段 n 次的参数曲线
B样条曲线是分段构成的,所以控制多边形对曲线的控制灵活直观。若给定m+n+1个控制点,可以构造一条n次B样条曲线,它是由m+1段n次曲线首尾相接而成,而每段曲线则由n+1个顶点所构造。
三、B样条曲线的推导
1. 一次B样条曲线
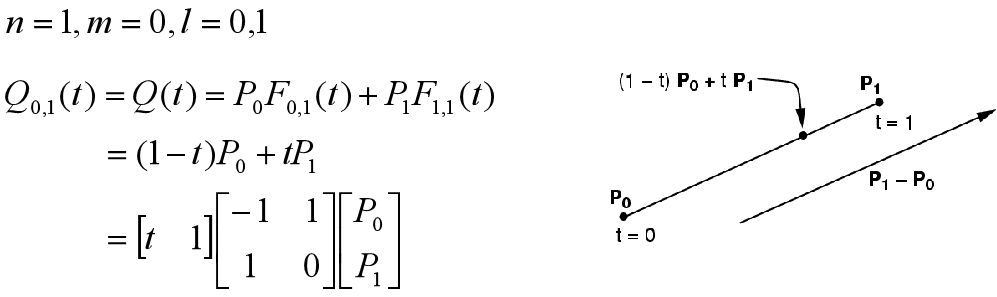
2. 二次B样条曲线
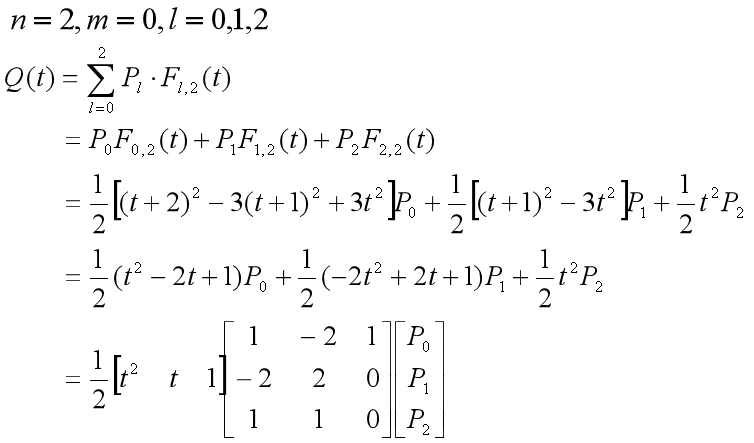
二次B样条曲线为抛物线:
二次B样条曲线的性质:
1)端点的位置:起点在P0P1的中点; 终点在P1P2的中点
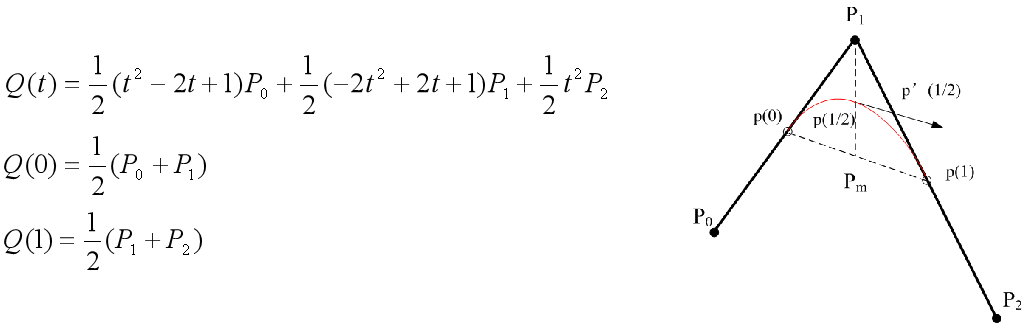
2)端点的切实量:起点处的切矢量为P0P1 ; 终点处的切矢量为P1P2
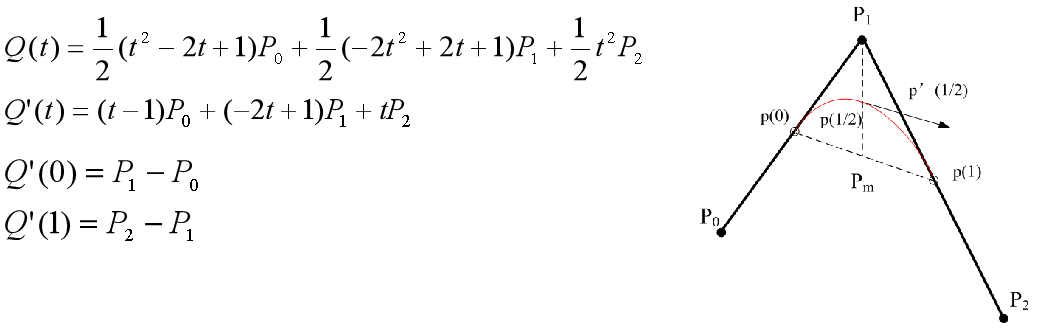
3)局部性:每一段二次B样条曲线受三个控制点的影响,修改一个控制点的位置只影响三条曲线的形状。
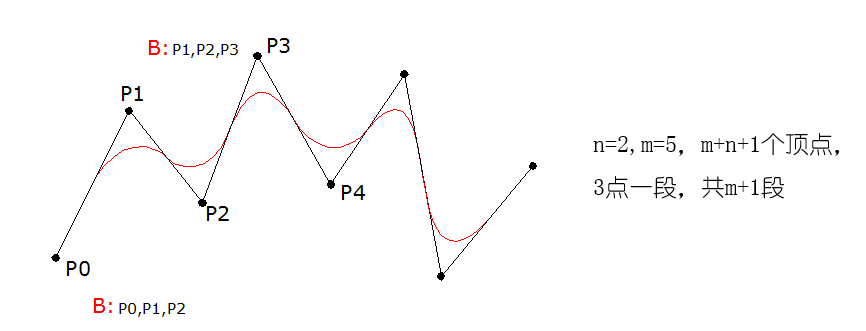
4)自动连续性:
自动保持光滑连接:每在控制点序列中添加一个点都会多生成一段B样条曲线,且与原曲线保持C1连续
5)凸包性
6)几何不变性
3. 三次B样条曲线

三次B样条曲线表示的曲线:
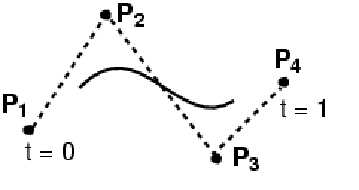
三次B样条曲线的性质:
1)端点的位置:起点在![]() 的1/3处; 终点在
的1/3处; 终点在![]() 的1/3处
的1/3处
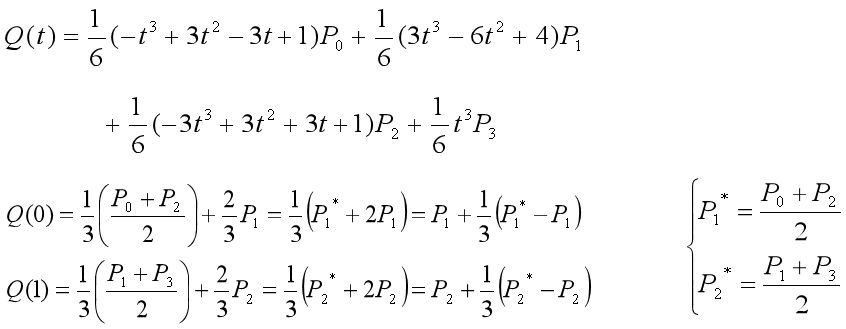
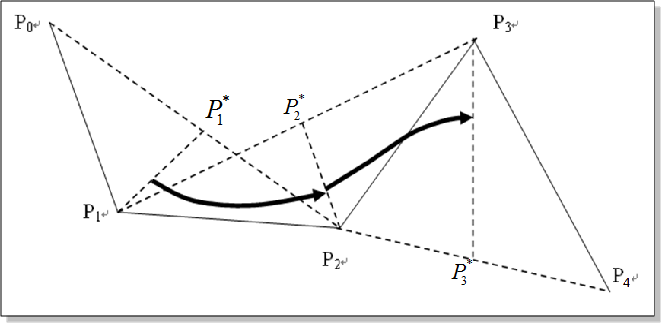
2)端点的切实量:
起点处的切线矢量平行于P0P2,长度为其一半; 终点处的切线矢量平行于P1P3,长度为其一半
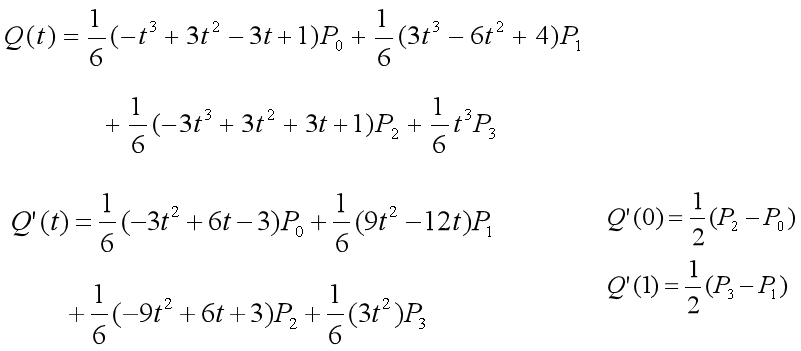
3)局部性
每一段三次B样条曲线受四个控制点的影响,修改一个控制点的位置只影响四条曲线的形状。
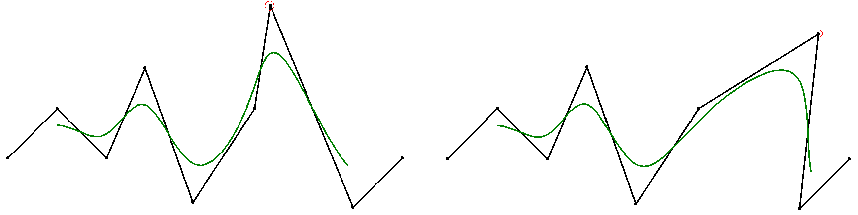
4)自动连续性
5)凸包性
6)几何不变性
四、B样条曲线的绘制

