一、光栅化概念

图元光栅化

    --  图元：图形学中不再分的独立图形，如点、直线、圆弧、多边形、字符、位图等 

    --  图元生成：完成图元的参数表示形式到点阵表示形式的转换，即图元的扫描转换（图元的光栅化）

    --  图元光栅化：光栅扫描显示器的绘图过程就是在像素点阵中确定最佳逼近于理想图元的像素点集，并用指定颜色显示这些像素点集的过程

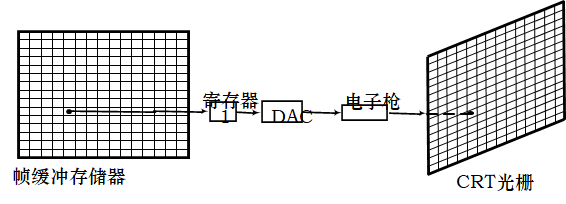
直线光栅化（直线扫描转换）

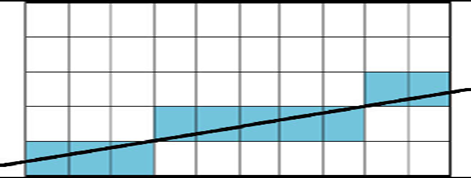
    --  在显示器给定的有限个像素矩阵中，确定最佳逼近该直线的一组像素，并且按照扫描线顺序对这些像素进行写操作。

--  直线光栅化要求

1.直线要直

2.直线的端点要准确，即无定向性和断裂情况

3.直线的亮度、色泽要均匀

4.画线的速度要快

5.直线可有不同的色泽、亮度、线型等

    --  直线光栅化方法

1.公式直接绘制法

2.数值微分法（DDA）

3.Bresenham法

4.中点画线法

二、直线光栅化

1.公式直接绘制法

基本原理：根据公式，依次计算直线上的点，并进行绘制

确点：浮点运算，耗费资源

2.数值微分法DDA（ Digital Differential Analyzer ）

直线的微分方程表示：

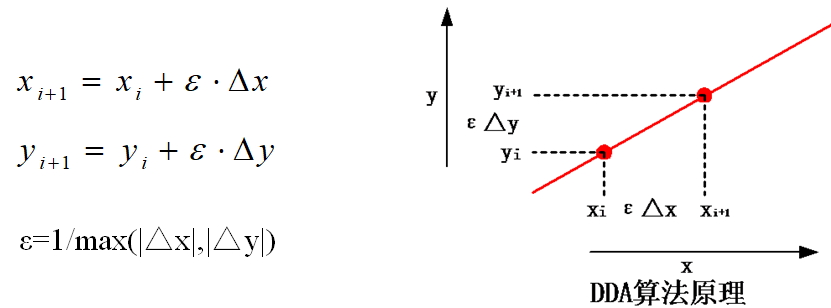
DDA算法原理分析（0≤k≤1）：

• 直接计算：将x按照步长=1(像素)递增，求y=kx+b的值，并且取点(x,round(y))作为绘制的像素点的坐标，此时进行一个乘法、一个加法

• DDA：将x的步长设为    ，则通过如下计算将算法减为一个加法实现。

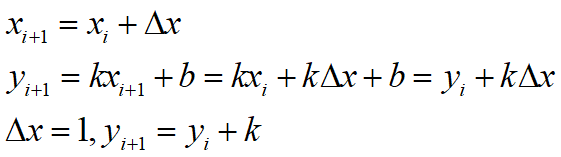
（1）DDA算法实现（0≤k≤1）：

（2）任意区间DDA算法实现

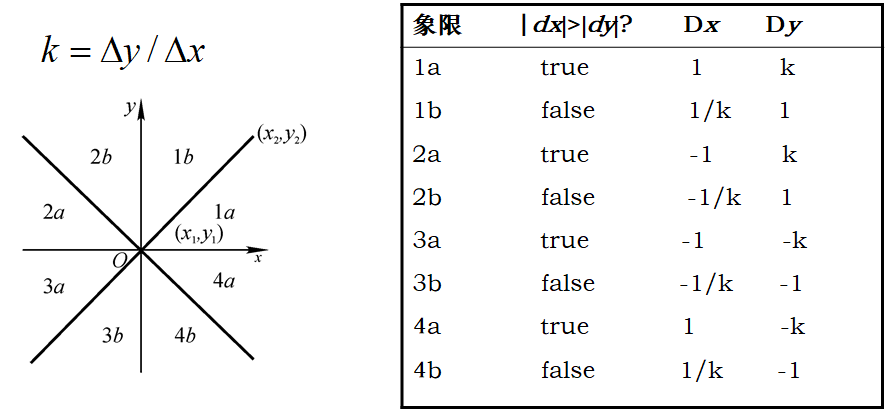
3.Bresenham画线法

基本原理(0≤k≤1)：直线与垂直网格线求交点，求与交点最近的象素。假设Pi 为当前像素，下一个离直线最近的像素，或者是正右方点S，或者是右上方点T 。根据S和T分别到实际交点的距离s和t的大小决定选哪个点。

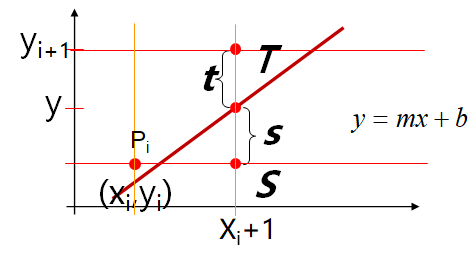
定义：

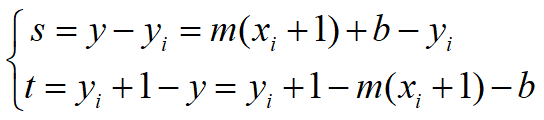
选择： s>=t 选 T ， s<t   选 S。

问题：选定S(T)之后，下一次该旋转的点如何判定？ 根据判别式符号，依次选择点亮的像素点。

1）定义判别式di：

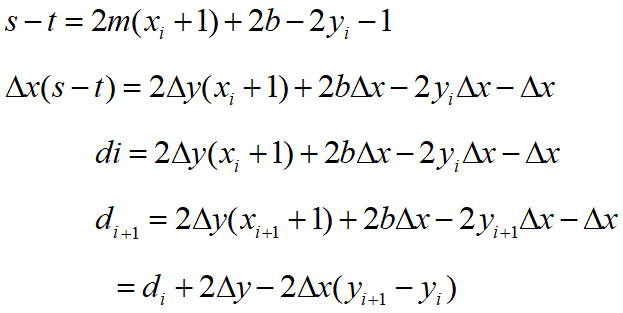
2）根据di符号，决定选取的像素点，及下一次的判别式：

  若di>=0，选T,di+1=di+2(△ y- △ x)

  若di<0， 选S,di+1=di+2 △ y

3）计算di的初值：d0=2 △ y- △ x

推导如下：

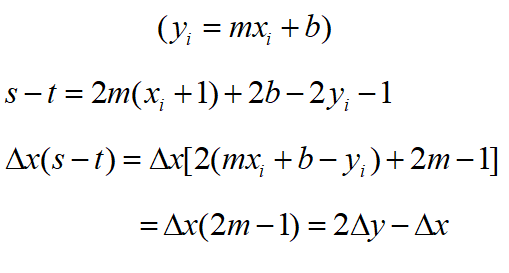
4）算法实现（1a区间）

5）算法实现（任意斜率直线）