一、变换的概念
一、图形变换的概念
图形变换:指图形的 几何信息 经过 几何变换 后产生新图形的变换
几何变换(建模变换):只改变组成形体的几何元素的几何信息(大小、形状、相对位置),而不改变图形 拓扑信息 的变换
图形变换的两种实现方法:
1)坐标系不动,图形变动—图形学采用
2)图形不动,坐标系变动--OpenGL采用
二、二维基本几何变换
基本几何变换:是相对于坐标原点和坐标轴的平移、旋转、缩放(变比)
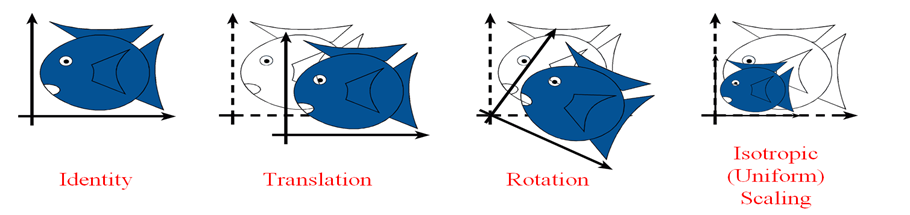
变换中点向量的表示:
向量表示:行向量 -- ![]() ;列向量 --
;列向量 -- ![]()
变换中矩阵的表示:
行向量 -- ![]()
列向量 -- 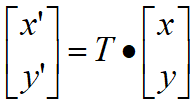
1. 二维平移
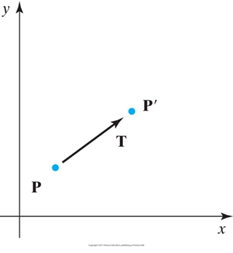
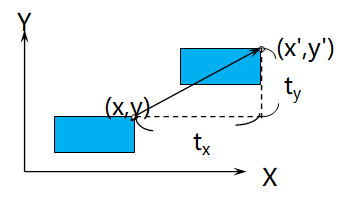
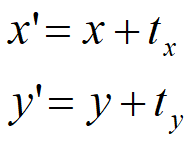
![]()
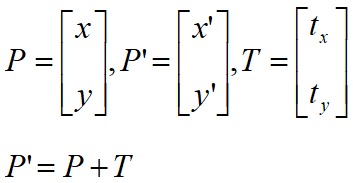
2. 二维旋转
绕指定点旋转指定角度
-- 已知旋转中心、旋转角度
-- 定义:旋转角度 – 逆时针为正; - 顺时针为负
基本旋转假设:旋转中心为坐标原点,旋转角度逆时针为正
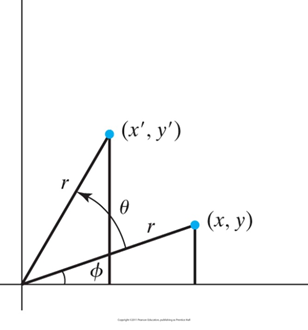
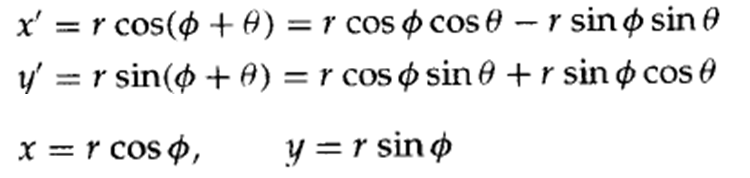
![]()
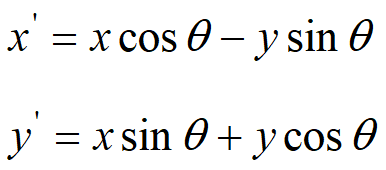
表示成矩阵相乘的形式,如下:
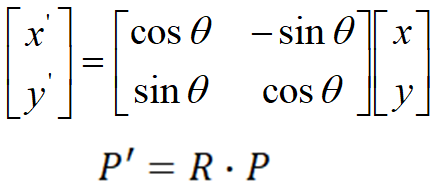
3. 二维缩放
基本缩放假设:相对于坐标原点的缩放,即改变图形大小和形状,也改变图形与坐标原点的距离
![]()
![]()
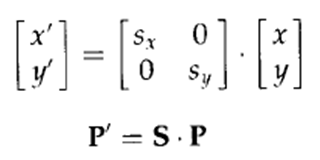
简单缩放的常见形式:

Sx = Sy =1 恒等变换
Sx = Sy ≠1 等比变换
Sx ≠ Sy 非等比变换,产生畸形
当比例因子Sx或Sy小于0时,对象不仅变化大小,而且分别按x轴,或y轴被反射(对称)
三、二维几何变换的统一形式 -- 齐次坐标
二维基本几何变换的变换矩阵,平移变换利用矩阵的加法实现,旋转、缩放变换利用矩阵的乘法实现。能否将所有变换的实现利用矩阵的统一运算实现?答案是可以的,但需要引入齐次坐标。

1. 齐次坐标的定义
-- Maxwell.E.A在1946年从几何的角度提出,20世纪60年代被应用于图形学。
-- 齐次坐标的基本思想:将n维空间的几何问题转换到n+1维空间去解决。
-- 定义:用一个有n+1个分量的向量去表示一个有n个分量的向量的方法称为齐次坐标
齐次坐标的表示形式:
二维点:p(x,y)对应的齐次坐标点:p(hx,hy,h)
h是任一不为0的比例系数。当h=1时,称为规格化齐次坐标。
普通坐标与齐次坐标的关系为“一对多”
给定一个点的齐次坐标表示: (x,y,h),该点的二维笛卡儿直角坐标: (x / h,y / h)。
齐次坐标的优势:
1) 提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。 (不改变点集的拓扑关系)
2) 便于表示无穷远点。
3) 变换具有统一表示形式,便于变换合成和硬件实现
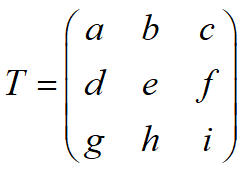
2. 齐次坐标表示的二维基本几何变换

二维基本几何变换的通式
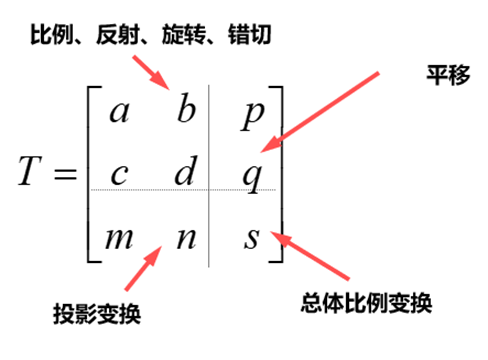
四、二维复合变换
复合变换的定义:
-- 任意一个变换序列均可表示为一个复合变换矩阵。
-- 复合变换矩阵可由基本变换矩阵的乘积求得。
-- 由若干基本变换矩阵相乘,求得复合变换矩阵的方法称为矩阵的级联(矩阵的合并)
![]() --其中,M称为复合矩阵
--其中,M称为复合矩阵
1. 二维复合平移
连续两次平移,即将平移距离相加:

![]()
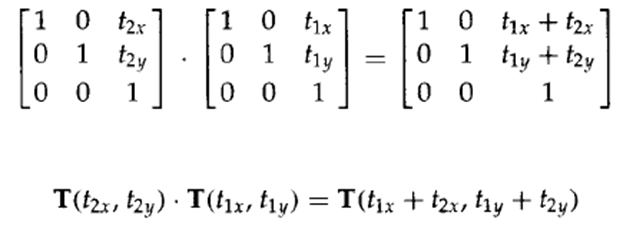
2. 二维复合旋转
连续两次旋转,即将旋转角度相加:
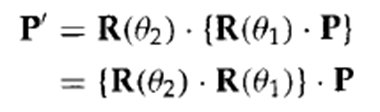
![]()
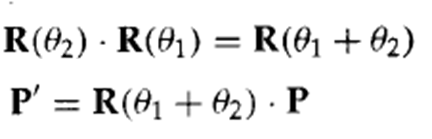
3. 二维复合缩放
连续两次缩放,即将缩放比例相乘:
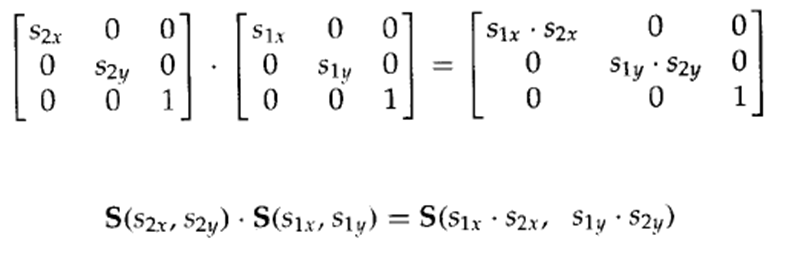
4. 相对于任意参考点的旋转
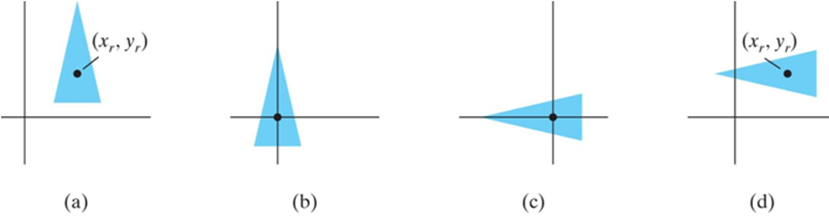
1) 平移:将变换的参考点移至坐标原点
2) 变换:进行旋转变换
3) 反平移:将参考点移至原来位置

5. 相对于任意参考点的缩放
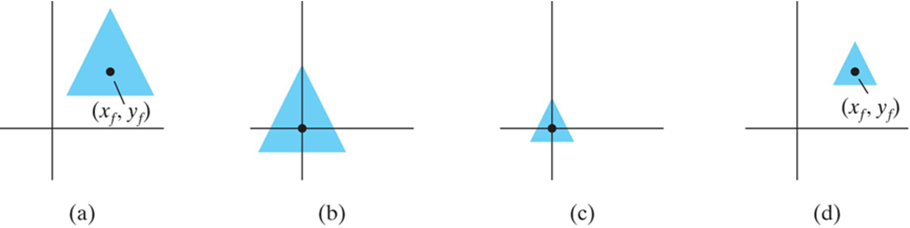
1) 平移:将变换的参考点移至坐标原点
2) 变换:进行缩放变换
3) 反平移:将参考点移至原来位置
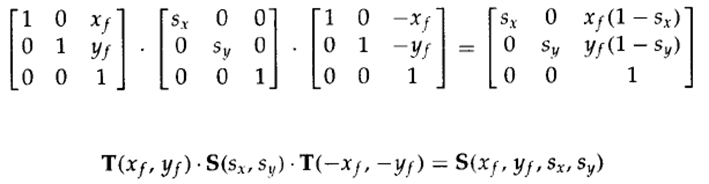
6. 复合变换的变换顺序
复合变换,是有序变换,顺序不可随意 --- 矩阵乘法不满足交换律
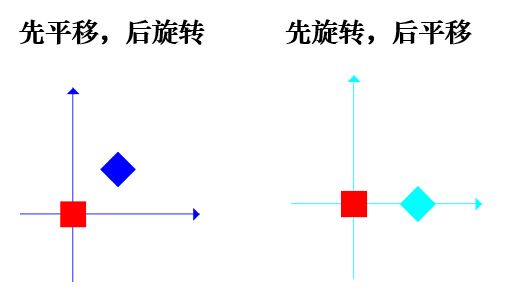
五、二维反射(对称)变换
-- 反射是用来产生物体的镜像的一种变换。
-- 物体的镜像一般是相对于一个对称轴生成的。
1. 相对于x轴的对称变换
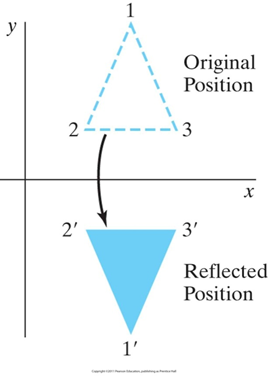
![]()
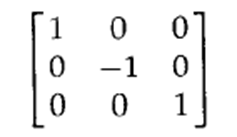
2. 相对于y轴的对称变换
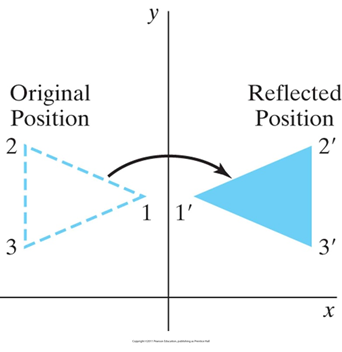
![]()
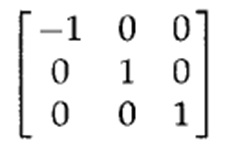
3. 相对于坐标原点的对称变换
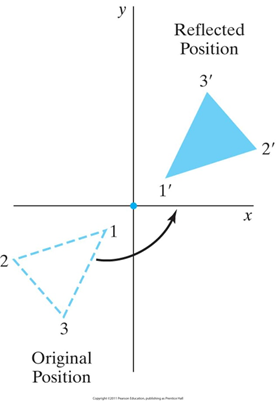
![]()

4. 相对于直线y=x的对称变换
方法一:
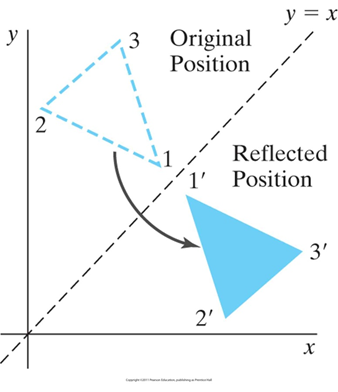
![]()

方法二:复合变换
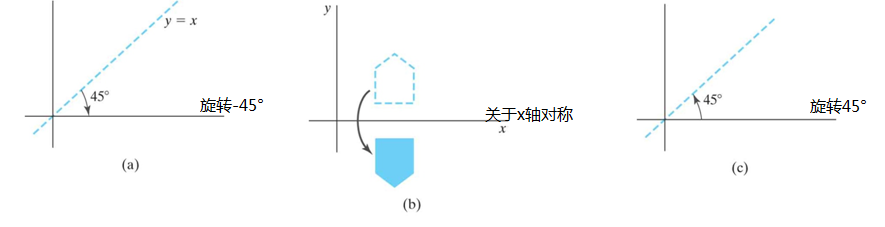
5. 相对于直线y=-x的对称变换
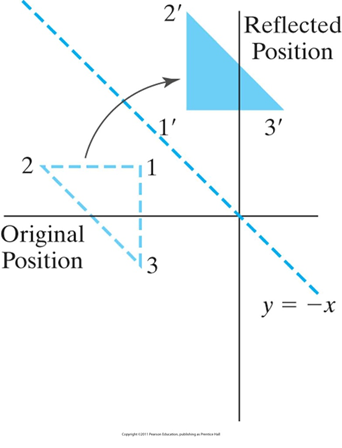
![]()

6. 相对于任意直线的对称变换
直线表示及图示:
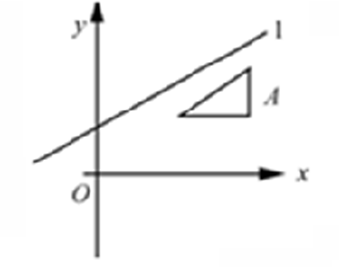
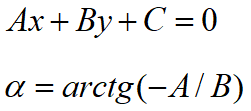
复合变换过程描述:
(1)平移使直线过原点;
(2)绕原点顺时针旋转α角,使 直线与x轴重合;
(3)关于x轴作对称变换;
(4)绕原点逆时针旋转α角;
(5)逆平移使直线回到原位置。
复合变换过程图示及变换矩阵:
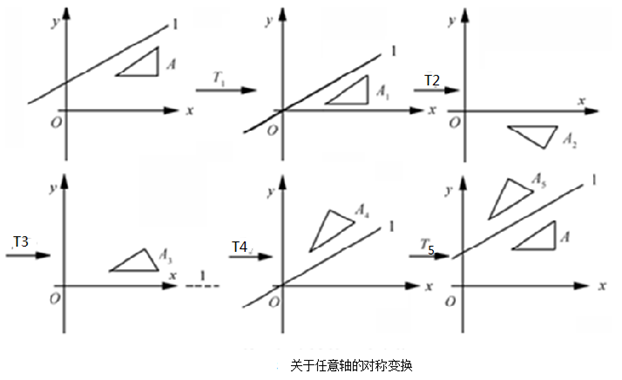
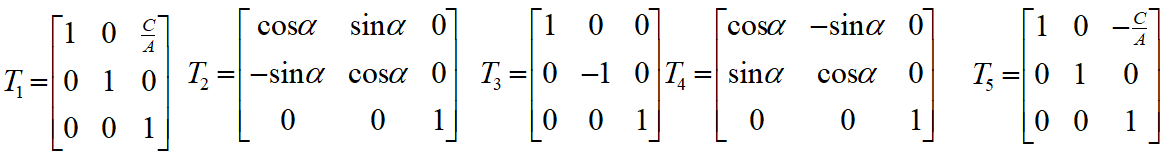
复合变换矩阵:
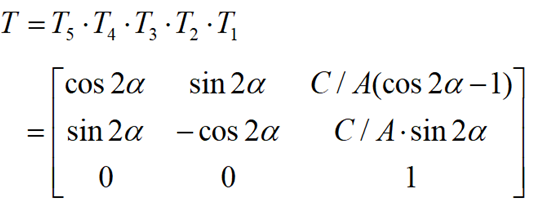
六、二维变换的应用 -- 坐标变换
1. 二维坐标系间的变换
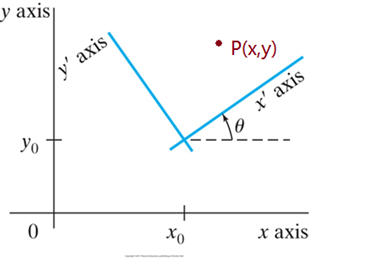
-- 已知:两个直角坐标系(xoy)和(x’oy’) 。其中, (x’oy’)坐标系的坐标原点是(xoy)坐标系的点(x0,y0),x’坐标轴与x坐标轴间夹角为
-- 问题:设(xoy)中一点p(x,y),求该点在坐标系(x’oy’)中的坐标p’(x’,y’)

2. 视口变换
裁剪窗体:确定场景的可见区域;
视口:确定场景的显示区域
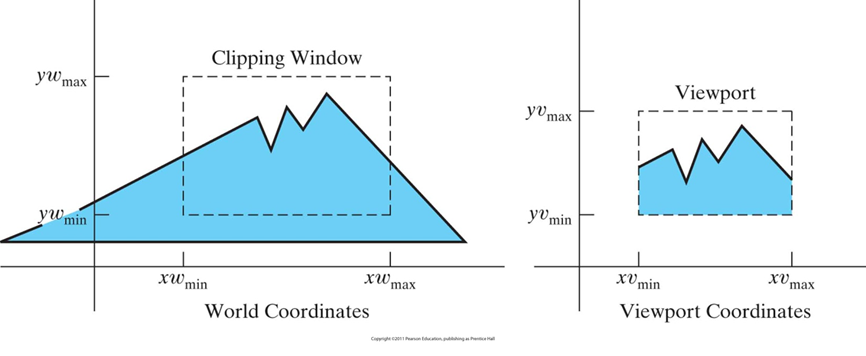
将位于裁剪窗体内的对象,显示在用户定义的视口内,期间需要经过平移变换、缩放变换。假设裁剪窗体的定义、视口的定义如下图所示:
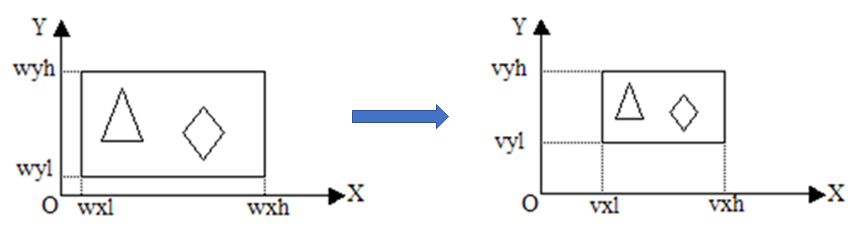
具体变换过程如下:
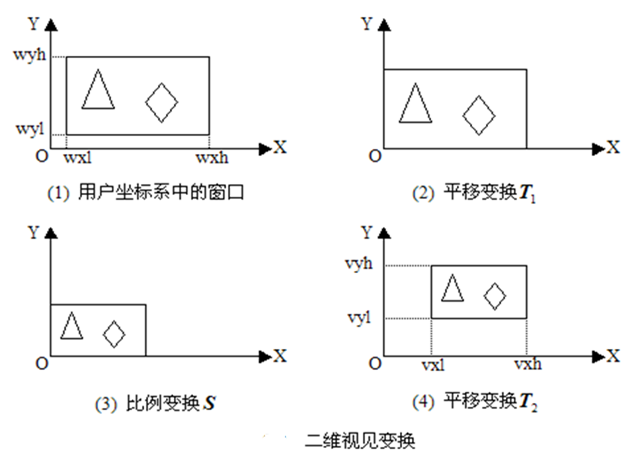
变换矩阵如下: