面剔除   ---   凸多面体消隐

一、算法思想

根据欧拉定理，如果多面体在它们每一个面所决定的平面的同一侧，则称此多面体为凸多面体，一个凸多面体的表面可连续地变形为一个球面，则称之为简单多面体。简单多面体有其自身的特性：在投影关系上，体的表面要么完全可见，要么完全不可见；各朝向面均不发生相互重叠现象

可以利用形体表面外方向量和视线向量之间的关系，确定表面可见性。形体表面（外）法向量为由形体内部指向外部，或由形体表面指向外部空间。给定视点的位置确定视线向量，根据表面法向量，我们可以判断出当前表面的可见性。当视线向量与表面法向量之间夹角小于90度时，相应表面可见；当视线向量与表面法向量之间夹角大于90度时，相应表面不可见。如图所示，确定了视线向量和表面法向量之后，表面可见性即可给出。

根据向量点积，可得，

根据两个向量夹角余弦值进行判断，当，即时，相应表面Pi 为朝前面，是可见面，应该画出；当，即时，相应表面Pi 为朝后面，是不可见面，不被画出或用虚线表示。

二、算法加速

假设   --  视线矢量平行于某一基本坐标轴

当视线矢量vi 平行于某一基本坐标轴时，那么平面的外法矢量n{A，B，C}与视线矢量的夹角就是外法矢量n与某一基本坐标轴的夹角，分别用α、β、γ 表示视线矢量平行X、Y、Z 轴时平面的外法矢量n{A，B，C}与坐标轴的夹角。

如果当前视线矢量平行于z坐标轴，则视线矢量与z轴之间夹角余弦值可简化为

这时夹角余弦值的符号取决于外法矢量n{A，B，C}在z方向上的分类C：那么，当C>=0时,当前平面可见；当C<0时,当前平面不可见；

同理，当视线矢量平行于X轴时，某平面的可见性由该平面外法矢量n在X轴方向上的分量A的符号决定。

当视线矢量平行于y轴时，某平面的可见性由该平面外法矢量n在Y轴方向上的分量B的符号决定。

三、平面外发矢量计算

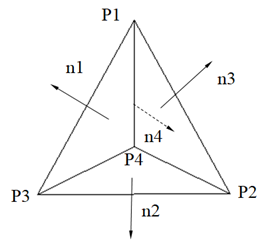
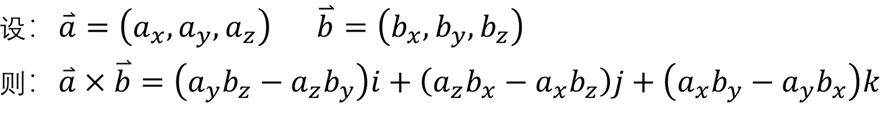
四、 单个凸多面体消隐算法步骤（视线矢量平行坐标轴）

1） 根据表面的数据结构，取顶点数据，计算表面的外法线矢量。

 2）计算外法线在投影方向上的分量的值。  

 3）根据分量的值判断表面的可见性。

 4）若表面可见画出该表面，否则处理下一个表面