检索结果共
个
3.1
第三章 现代物理学
3.1.1
第一节 狭义相对论
3.1.1.1
一、 义相对论的两条基础原理
3.1.1.2
二、狭义相对论运动学的核心——洛仑兹变换
3.1.1.3
三、狭义相对论时空观
3.1.1.4
四、狭义相对论力学
3.1.2
第二节 广义相对论
3.1.3
第三节 量子力学
3.1.4
第四节 现代物理学的新进展
3.2
第四章 现代数学
3.3
第五章 现代化学和生物学
3.4
第六章 现代地学、天文学和宇宙学
3.5
第七章 系统科学
友情提示：同学您好，此页面仅供预览，在此页面学习不会被统计哦！ 请进入学习空间后选择课程学习。
（四）狭义相对论力学
（1） 相对论质量
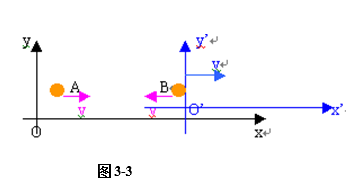
讨论：Σ系中质量为m0的A球以V沿x方向运动，相对Σ系以V运动的Σ’系上有同样的球B以相对Σ’系ux’= -V运动，两球相碰发生完全弹性碰撞，如图：
根据对Σ系由动量守恒：（m+m0）ux=mv
对Σ’系由动量守恒：
（m+m0）ux’= - mv，速度变换式：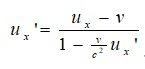
解这几个方程就得到：m= ץ m0 ，竟然速度ｖ增加（ץ增加）质量ｍ也要增加。
（2）相对论质能关系
讨论：单个粒子在外力F作用下移动一段路程使得动能从0→EK。
根据动能定理：A=ΔEK
牛顿定律：
质速关系：m= m0
推导：Ek=Ek-0=ΔEK=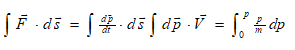
由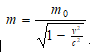
→ m2c2-p2= m02c2→ pdp= mc2dm代入上式得：
EK=
显然，粒子的总能量为：E=mc2
粒子的静止能量为：E0=m0c2
粒子的动能为：EK=mc2 – m0c2=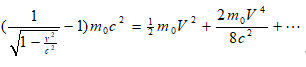
可见粒子的动能不等于经典的形式，但当V<<c时，EK≈mV2/2
（3）相对论力学方程
在经典物理中牛顿定律常把它写成
，现代物理证明这只在低速情况下近似成立，普遍的形式是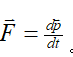
。实际上这是力的定义式。力是物体整体运动状态变化的原因，用P来表示状态参量要比用V周全，因为V仅仅表示了物体相对运动因素，而P=mv表示了物体整体作相对运动时运动的完整数量。