检索结果共
个
3.1
第三章 现代物理学
3.1.1
第一节 狭义相对论
3.1.1.1
一、 义相对论的两条基础原理
3.1.1.2
二、狭义相对论运动学的核心——洛仑兹变换
3.1.1.3
三、狭义相对论时空观
3.1.1.4
四、狭义相对论力学
3.1.2
第二节 广义相对论
3.1.3
第三节 量子力学
3.1.4
第四节 现代物理学的新进展
3.2
第四章 现代数学
3.3
第五章 现代化学和生物学
3.4
第六章 现代地学、天文学和宇宙学
3.5
第七章 系统科学
友情提示：同学您好，此页面仅供预览，在此页面学习不会被统计哦！ 请进入学习空间后选择课程学习。
（二）狭义相对论运动学的核心——洛仑兹变换
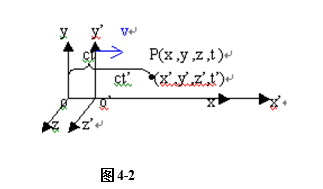
有了这两个新的公理，则非常重要的洛仑兹变换关系就非常自然的推导出来了。讨论一个从t=0 x=0发出的光子在Σ系和Σ’系（在t=0时Σ’系与Σ系重合，以后Σ’以V沿X轴方向运动）中的情况,根据：
（1）时空均匀性：x=ץ(x’+vt’)
（2）相对性原理：x’= ץ(x - vt)
（3）光速不变原理：x=ct,x’=ct’
其中：时空均匀性条件不是新的原理，一个固定的物体放在空间任意位置无论何时长度是相同的这是非常直观的，由简单的推理可知均匀时空的坐标变换是线性的。因为若设：x=ax’2+bt’,则任一瞬间（dt’=0）测量一物体长度：dx=2ax’dx’。可见对Σ’系任意一个dx’放在不同的x’，对Σ系来说是长度不同的，也即对Σ系空间是不均匀的这不符合直觉。因Σ’与Σ是等价的，Σ’系变到Σ系有x=γ(x’+vt’)，则Σ系变到Σ’就一定有x’=γ(x - vt)，可见相对性原理对不同的惯性系是公平的。最后由光速不变原理给出的两个关系，看起来费解，却有实验支持，这们联立以上4个方程并求解就立即可得到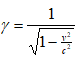
和洛仑兹变换：
Σ’系→Σ系 Σ系→Σ’系
x=γ(x’+vt’) x’= ץ (x - vt)
y=y’ y’=y
z=z’ z’=z
t=γ(t’+vx’/c2) t’= ץ (t-vx/c2)
洛仑兹变换统一了时空和运动，统一了高速世界和经典力学研究的低速情况。当ｖ<<c时γ=1即洛仑兹变换变成了伽俐略变换。