3.1 数值类型知识点  3.2 整数:
3.2 整数:
整数的表示方法:整数是不含小数点的数字,可使用四种不同的进制进行表达。
注意:整数的表示范围--Python 3 中整数在计算机内是精确表示的,大小几乎没有限制,可以存储内存能够容纳的无限大整数(整数大小只受到内存容量的限制),这与其他程序设计语言中的整数有很大区别。
3.3 浮点数
1、浮点数的两种表示方法:小数形式(十进制)和指数形式(科学计数法)
小数形式:由整数部分、小数点与小数部分组成。其小数部分可以没有数字,但必须有小数点,此时相当于小数部分为0
指数形式:采用科学记数法表示为<a>e <n>,等价于数学中的a×10n
2、浮点数的表示范围和表示精度
浮点数使用8 个字节(64 位)的存储空间
浮点数表示的数字范围为1.7× 10-308~1.7× 10308
超过浮点数的表示范围时,会触发溢出异常(OverflowError)
与整数不同,浮点数的表示是不精确的,浮点数默认提供大约17位数字的精度(由计算机存储机制决定),输出时浮点数将只保留16或17位有效数字。浮点数超出精度的数据存储时会被丢弃
3.4 复数
复数(Complex):由实部a和虚部b 构成
表示方法1:a + bj
表示方法2:complex(a, b)
复数的实部a 和虚部b都是浮点数
用real和imag分别获取复数的实部和虚部
用abs(a+bj)获得复数的模
3.5 数值类型转换
程序中,要进行不同数值类型的转换,可将数据类型作为函数名,将要转换的数字作为函数的参数即可完成转换。
1、int(x) :将浮点数 x 或整数类型字符串转换为一个整数
语法:int( x, [base=10])
说明:int(x) 将浮点数 x 或整数类型字符串转换为一个整数。
第一种情况:当x是一个浮点数,不需要使用参数base,这时int函数会将浮点数转换成十进制整数(取整原则是向0取整)。
第二种情况:当x是一个十进制整数类型的字符串时,不需要使用参数base,这时int函数会将字符串转换成十进制整数;而当x是一个2、8、16进制整数类型的字符串时,可使用参数base指明是几进制整数类型的字符串(base=0,则系统根据字符串的前缀引导符确定该数的进制),以帮助int函数最终将其转换成十进制整数。
需要注意的是,int函数只能将整数字符串或浮点数转成整数,而不能将浮点数字符串转成整数。
2、float(x) :将整数 x 或浮点数类型字符串转换为一个浮点数
语法:float( x)
说明:float(x) 将整数 x 或浮点类型字符串转换为一个浮点数。
3、eval(x):将数值型的字符串对象x 转换为其对应的数值
语法:eval( x)
说明:eval(x)将数值型的字符串对象x 转换为其对应的数值,及整型字符串转为整数,浮点类型字符串转为浮点数。此外,eval(x)可将逗号分隔的多个数值型数据的字符串转换为一个元素为数值类型的元组,利用该特性,可以实现在一条语句中将用逗号分隔的多个数值型数据分别赋值给不同的变量,以实现多变量的同步赋值。
4、complex(x[, y]) :将x 和y 转换为复数,实数部分为 x,虚数部分为y
complex(x) :将 x 转换为复数,实数部分为 x,虚数部分为 0
3.6 运算符和表达式

1、算术运算符

算术运算符的优先级:①** ;②*、/、%、//;③+、-
可以使用括号改变优先级,或提高程序的可读性
3.7 常用数学运算函数

3.8 math模块及其应用
模块(Module):模块本质上是一个Python程序,以py作为文件扩展名,任何一个包含Python定义和语句的py文件都可以作为一个模块。
通过使用模块,不仅可以有效避免命名空间的冲突,还可以将一个较大的程序分为多个文件,提升代码的可重用性、可维护性。
编写Python程序时,经常会使用他人编写好的模块。有些模块不需要额外安装就可以直接使用,这样的模块称为标准库。没有纳入标准库的模块,需要安装后才能使用,安装命令如下:
pip install 模块名/库名
Python中没有定义库的概念,库是对模块和包的通俗说法,是借用其他编程语言中的习惯叫法而已。例如math模块也称math库。
要在代码中使用某个模块,首先必须导入它。模块的导入有两种方法:
方法一:import <库名>
使用第一种方法导入库,调用库中的函数时,函数名前加库名。
方法二:from <库名> import <函数名1,函数名2,...,函数名n> 或: from <库名> import * (*号 是通配符,表示导入库中的全部函数)
使用第二种方法调用库中函数时,函数名前不需加库名。
3.9 程序举例
示例1:计算弓形的面积
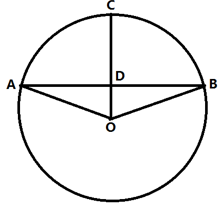
问题:AB是圆的一条弦,ABC形成一个弓形,在两行中分别输入AB和CD的长度,计算弓形的面积。结果保留小数点后2位有效数字。

示例2:计算学分、学费和贷款额度
