全屏显示课程章节

自动控制原理

王晓慧青岛大学

检索结果共个

自动控制系统的基本概念

1.1 课前预习

1.2 自动控制及自动控制理论的发展

1.3 自动控制的基本原理与方式

1.4 自动控制系统的分类

1.5 对自动控制系统的基本要求

1.6 拓展阅读-自动控制理论发展综述

1.7 拓展阅读-智能控制理论及应用综述

1.8 单元测试

自动控制系统的数学描述方法

2.1 课前预习

2.2 控制系统的微分方程

2.2.1 线性微分方程的求解

2.3 传递函数

2.4 动态结构图化简与梅森公式

2.5 控制系统的几种常用的传递函数

2.6 拓展阅读-300MW机组过热蒸汽温度控制系统建模与仿真

2.7 单元测试

控制系统时域分析

3.1 课前预习

3.2 典型的输入信号和时域性能指标

3.3 一阶系统的时域分析

3.4 二阶系统的时域分析

3.5 控制系统的稳定性分析

3.6 控制系统的误差分析

3.7 拓展阅读-基于线性系统时域分析法的婴儿培养箱温控评价研究

3.8 拓展阅读-一种无人机多舵面同步时域分析方法

3.9 单元测试

控制系统的根轨迹分析

4.1 课前预习

4.2 根轨迹的概念与根轨迹方程

4.3 根轨迹的基本原则和方法

4.4 用根轨迹分析控制系统

4.5 根轨迹改造

4.6 拓展阅读

4.7 单元测试

控制系统的频域分析

5.1 课前预习

5.2 频率特性

5.3 典型环节的频率特性

5.4 系统的开环频率特性

5.5 频域法分析闭环系统的稳定性

5.6 用开环频率特性分析系统性能

5.7 拓展阅读

5.8 单元测试

控制系统校正

6.1 课前预习

6.2 系统校正概述

6.3 串联超前校正

6.4 串联滞后校正

6.5 串联滞后超前校正

6.6 串联校正的期望特性法

6.7 PID校正装置及PID串联校正

6.8 反馈校正

6.9 拓展阅读

6.10 单元测试

友情提示：同学您好，此页面仅供预览，在此页面学习不会被统计哦！请进入学习空间后选择课程学习。

第二章自动控制系统的数学描述方法

课程导入：

1.什么是数学模型？

数学模型是描述系统的输出变量与输入变量（或内部变量）之间关系的数学表达式。

2.为什么要建立控制系统的数学模型？

便于定量给出系统中一些变量之间的相互关系。从而对控制系统进行分析设计。

3.集中参数线性定常控制系统数学模型的形式有哪些？

微分方程、传递函数、动态结构图

线性系统满足叠加原理和齐次性。

4.如何建立一个控制系统的数学模型？

（1）机理建模：解析法，根据系统及元件各变量之间的物理、化学定律，列写出各变量间的数学表达式，从而建立数学模型。

（2）实验建模：实验法，对实际系统或元件加入一定形式的输入信号，通过辨识的方法，采用数学模型去逼近这个响应。

2-1 动态微分方程

1.微分方程的表示

系统的微分方程表示.png

2.建立系统微分方程的步骤

①确定系统的输入量，输出量。体现建模目的

②从输入端开始，按照信号的传递顺序，根据规律列写原始方程式，可提出必要的假设，以简化模型。

③消去中间变量，写出输入、输出变量的微分方程

④联立方程式，消去中间变量，整理方程将其标准化。

左边：输出量及各阶导数

右边：输入量及各阶导数

导数项阶数：从高到低

3.建立系统微分方程的例子

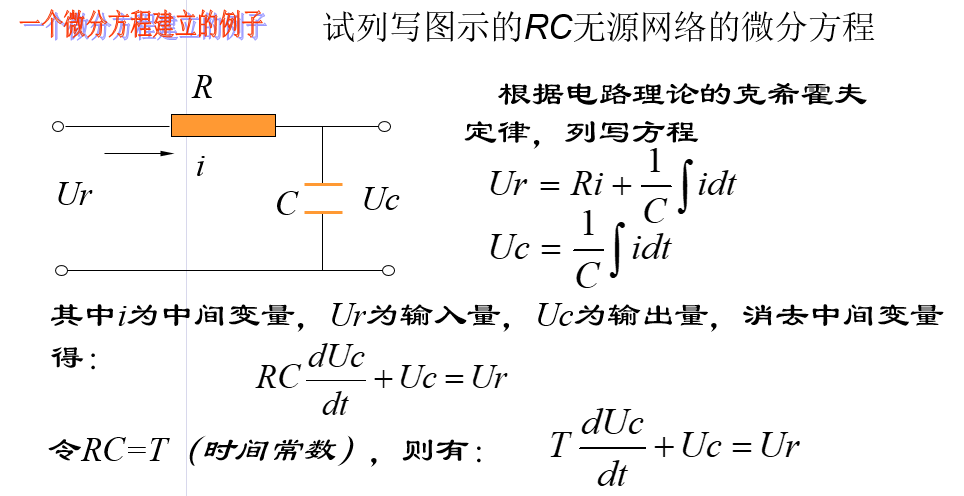
建立微分方程例1.png

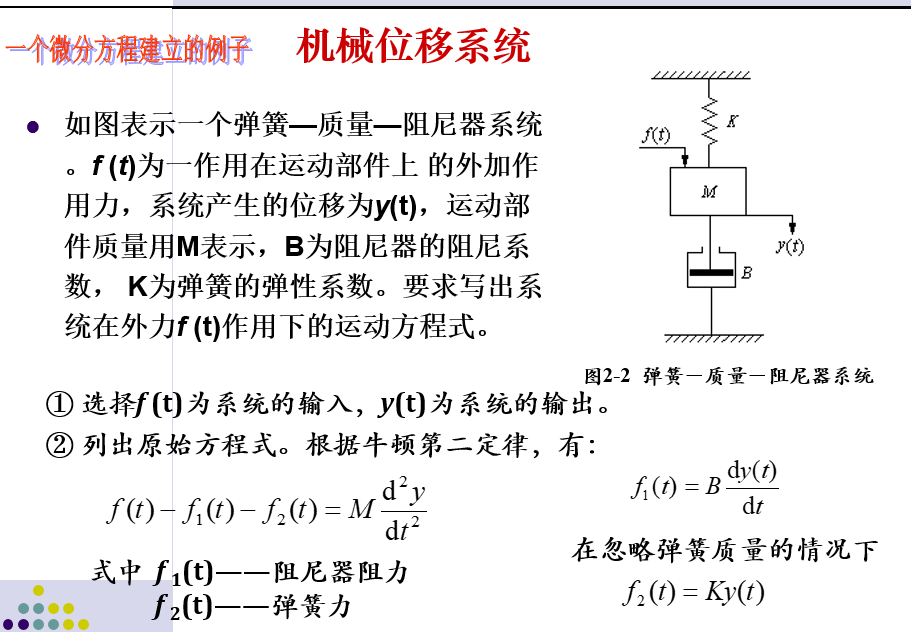
建立微分方程例2.png

注意：不同物理原件组成的系统，可以有相同的数学模型，它们内部的物理变化机制有相似性，它们是相似系统。